Simple Financial Ideas can get Complicated Mathematically

If we recorded the price of every trade for several hundred stocks for 10 years, we would have too much data. So we usually record only the high, low and closing price for the day. If I postulate a model, which says that there is some intrinsic price $p^*$, and that all trades during the day are noisy measurements of that intrinsic price, what is the best estimate of $p^*$?

Applying `order statistics' and `maximum-likelihood' estimation techniques, leads to a partial differential equation for the $\log$-likelihood function:

where $y_1^{}=(\mbox{High}-p^*)/\sigma$, $y_2^{}=(\mbox{Low}-p^*)/\sigma$, $y_3^{}=(\mbox{Close}-p^*)/\sigma$ and $Q$ is the standard error function. We have not been able to find a general solution to this equation.

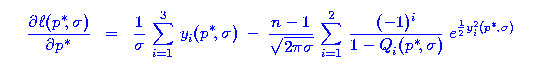
This is just one of many possible illustrations of simple financial ideas leading to complex mathematics.

  
Complex Mathematics, Pragmatism and Simple Solutions

But that is not the end of the indicative-price story. In the case of a frequently traded security, certain quite reasonable assumptions can be made. An approximate solution[ 2] is

ie. the average of the high and low for the day--an elegantly simple solution.

At first, it seems to be an uncomfortable solution because it involves `outliers' or extreme values. But every time a high is pushed a little higher by some new trade, the new high is based on additional information. Thus the high and the low are the two prices with the greatest information content. Once this is appreciated, the idea of using their average becomes intuitively appealing.

The solution is thus:

• based on a simple but realistic model;
• results from sound statistical tools;
• involves the pragmatism of reasonable approximations;
• results in an elegantly simple formula, which
• provides insight into the real processes at work;
• is intuitively reasonable; and
• (potentially) helps real traders make real money.

In many ways, it is a beautiful result.

(If prices are modelled as $\log$-normally distributed, the geometric mean replaces the arithmetic mean.)

  
Low-Tech Maths is also OK

When I first arrived at Lend Lease, its investment management performance had been reasonably good, but the inflow of funds had not been commensurate. A key, but mathematically simple, extension of a previous idea led to a very easily understood visual tool. Technically, one might call the graphs `Dynamic Relative Risk/Return Histories'[ 4]. The market has its own style for dealing with such technicalities; it has universally chosen to call them ``Snail Trails''[ 7], because of the meandering appearance of these graphs. Basically they show, at a glance, the value-adding and risk-reducing skills of a particular manager, over time and relative to the manager's peer-group. They have been widely accepted by the performance measurement community, and even by a number of our competitors. Introduction of this relatively low-tech tool has coincided with a distinct upturn in the growth of our flagship fund--from $900 million in early 1991 to over $4.5 billion last December!

  
New Mathematical Technology: Chaos Theory, Neural Nets & Genetics

There is much hyperbole surrounding the use of chaos theory, especially in finance. Ron Layard-Liesching of Pareto Partners in London has said that ``the best way to make money out of chaos theory is to write books on it.'' Ed Peters of PanAgora Asset Management in the USA, a prolific writer on the subject, tells me that ``if the hours spent writing are taken into account, even that is not true.'' Chaotic models are hyper-sensitive to errors in the initial conditions. If one accepts my model that traded prices are only noisy measurements of a true underlying price, then deterministic chaos is doomed in finance.

A colleague and I recently wrote a research paper entitled ``Artificial Neural Networks: Cerebrally smart but lamentably dumb''[ 11], in which we discussed the power of neural nets for nonlinear and robust modelling, but also pointed out some of their dramatic failures.

If applied intelligently and with great care, genetic algorithms show great promise for non-linear optimisation in finance. Their greatest virtue is their ability to find global maxima, provided sufficient genetic diversity is present in the initial population of solutions[ 5].