


Next:
Birthday Cards
Up:
2010 and all that
Previous:
2010 and other pretty
Yet more interesting cases are those for which the curve
occupies more than a finite region.
Pick any nasty irrational number;  is a good example.
Now let the rule for the angles be
is a good example.
Now let the rule for the angles be 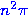 -- so the angles are
sequentially
-- so the angles are
sequentially  ,
, 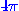 ,
, 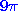 ,
, 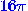 , ...revolutions.
, ...revolutions.
There are two difficulties in drawing the complete picture:
-
there are too many segments--infinitely many of them;
-
the complete picture takes up too much space--an infinite amount.
Nevertheless, what to do is clear.
Suppose we have just a few (say 10,000) segments in our field of view.
Now change the magnification of our microscope by pulling it away.
Then we may be able to see perhaps 100,000 segments;
but their detail is blurred.
What we actually can see is easily portrayed using just
some 10,000 `renormalised' segments.
Here are some of the first few renormalisations of  .
.
(Click images for a larger version.)


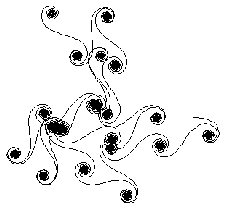
The preceding pictures are the 0 , 2
, 2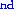 and 4
and 4 renormalisations of
renormalisations of  .
Each consist of some 4000 actual segments.
Now the third picture corresponds to many millions of segments
of the original
.
Each consist of some 4000 actual segments.
Now the third picture corresponds to many millions of segments
of the original  curlicue.
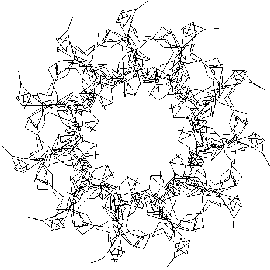
Indeed the first black `blob' on the right, together with its initial looping
tail, is its starting tens-of-thousands of segments. The first two pictures
are effectively magnifications of this portion.
curlicue.
Indeed the first black `blob' on the right, together with its initial looping
tail, is its starting tens-of-thousands of segments. The first two pictures
are effectively magnifications of this portion.
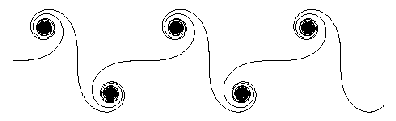

(Click images for a larger version.)



Next:
Birthday Cards
Up:
2010 and all that
Previous:
2010 and other pretty
Ross Moore ross@ics.mq.edu.au
1/28/1997






![]() , 2
, 2![]() and 4
and 4![]() renormalisations of
renormalisations of ![]() .
Each consist of some 4000 actual segments.
Now the third picture corresponds to many millions of segments
of the original
.
Each consist of some 4000 actual segments.
Now the third picture corresponds to many millions of segments
of the original ![]() curlicue.
Indeed the first black `blob' on the right, together with its initial looping
tail, is its starting tens-of-thousands of segments. The first two pictures
are effectively magnifications of this portion.
curlicue.
Indeed the first black `blob' on the right, together with its initial looping
tail, is its starting tens-of-thousands of segments. The first two pictures
are effectively magnifications of this portion.