TMATROM

A Matlab Object Oriented T-matrix Toolbox

About

News

License

Publications

Download

Contact

Issues

Example

About

Wave Scattering Toolbox

TMATROM is a simple and easy to use reduced order model toolbox for simulating 2D wave propagation

  • acoustic and electromagnetic waves
  • wave propagation exterior to one or more scatterers
  • sound soft/sound hard/ transverse electric (TE)/ transverse magnetic (TM)/ absorbing/ dielectric scatterers
  • low, medium and high frequencies

Reduced Order Model

TMATROM provides an easy to use reduced order model for wave propagation based on the T-matrix.

The T-matrix provides a low-dimensional highly accurate model for scattering by a particle for all incident waves e.g.

  • plane waves... any incident direction
  • point sources... any source location
  • reflected waves e.g. in multiple scattering

Applications

Faraday cage
Simulation of Faraday Cage using TMATROM.
The T-matrix ROM allows very efficient simulation of multi-parameter problems e.g.
  • monostatic radar cross section (RCS) computations
  • multiple scattering simulations
  • simulation of parameter dependent systems e.g. stochastic systems.

The user's own single particle scattering software can be easily extended for multiple scattering simulations using the ROM.

The ROM provides an instrument for different kinds of solver to talk to each other, allowing easy simulation of multiple scattering in systems with scatterers of mixed kind.

Numerical stability

The T-matrix is computed with the numerically stable algorithm in [2] using the far field. Rigorous mathematical analysis of the algorithm, including an a priori estimate for the ROM truncation error, was carried out in [3].

Numerical stability was demonstrated in [1] for several kinds of scatterer

  • nonspherical particles
  • high aspect ratio particles
  • large particles i.e. large EM/acoustic size parameter up to 300

shapediametererror
16 wavelengths 9.7e-9
16 wavelengths 1.0e-8
100 wavelengths 9.6e-9

A full convergence analysis for the T-matrix ROM is given in [3].

News

  • 24 Nov 2017 Some users reported a bug with the MPSPack examples. See the issues section below for the resolution.

License

TMATROM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

If you use this code, please cite:

M. Ganesh and Stuart C. Hawkins.
Algorithm 975: TMATROM-A T-Matrix Reduced Order Model Software.
ACM Transactions on Mathematical Software. Volume 44. Pages 9:1-9:18, 2017.

Related Publications

[1] M. Ganesh and Stuart C. Hawkins.
Algorithm 975: TMATROM-A T-Matrix Reduced Order Model Software.
ACM Transactions on Mathematical Software. Volume 44. Pages 9:1-9:18, 2017.
[2] M. Ganesh and Stuart C. Hawkins
A far-field based T-matrix method for two dimensional obstacle scattering.
ANZIAM. Volume 51. Pages C215-C230, 2009.
[3] M. Ganesh and Stuart C. Hawkins and R. Hiptmair
Convergence analysis with parameter estimates for a reduced basis acoustic scattering T-matrix method.
IMA Journal of Numerical Analysis. Volume 32. Pages 1348-1374, 2012.

Download

Version 2.2 Download all files (including documentation and examples):

Version 1 Download all files (including documentation and examples):

Contact

Issues

  1. 24 November 2017.
    Description: MPSPack examples exit with an error.
    TMATROM requires an extended version of MPSPack's scattering.gridfarfield method. To resolve this issue place the extended gridfarfield.m in the @scattering directory of your MPSPack installation.

Example

 We use TMATROM to simulate scattering of an incident plane wave by a sound soft scatterer described using polar coordinates (full code).

Create a scatterer

TMATROM provides several standard scatterer shapes eg circles, ellipses.

Other shapes can be created by the user. Here we create a trefoil shape using polar coordinates.

% anonymous functions for radius and its 1st and 2nd derivatives
r = @(t) 1 + 0.3 * cos(3*t);
dr = @(t) -0.9*sin(3*t);
ddr = @(t) -2.7*cos(3*t);
 
% create obstacle object
p = obstaclePolar(r,dr,ddr);

Visualise the scatterer

Once created we can visualise our shape.

% visualise the scattering obstacle
p.visualise()

The result looks like this: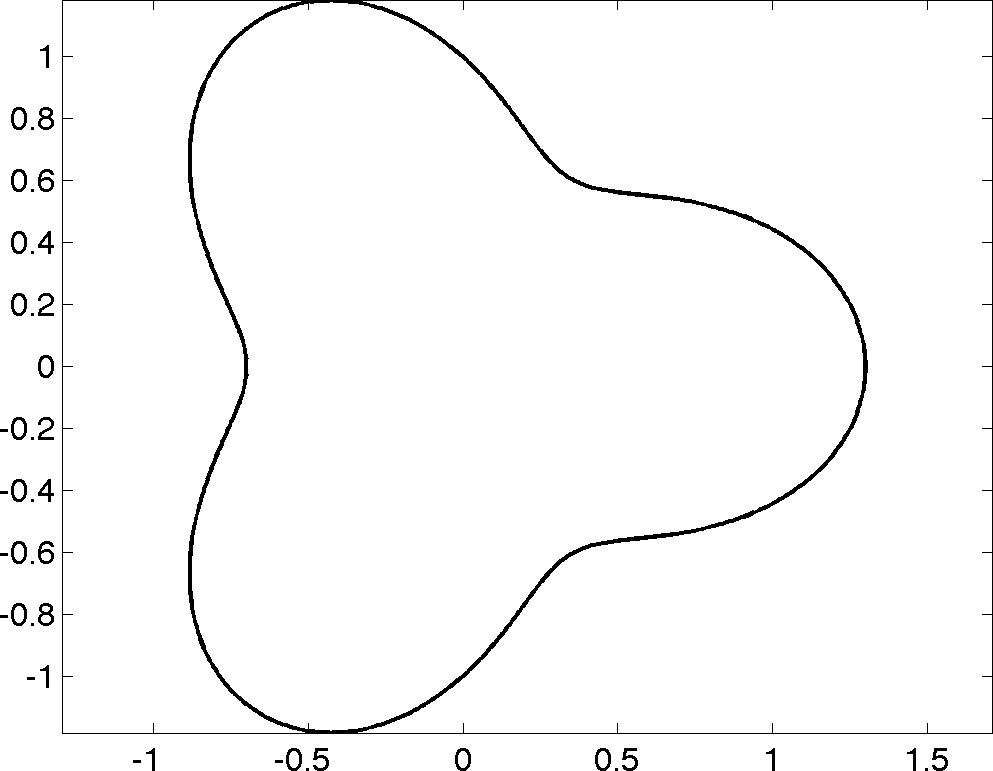

Setup the solver

Next we setup the farfield solver we use to compute the T-matrix.

For the trefoil scatterer, which has a smooth boundary, it is appropriate to use a Nystrom solver.

% set the wave number
kwave = 5;
 
% create the Nystrom (sound soft) solver object
solver = solverNystrom(kwave,[],p);
 
% set the Nystrom discretisation parameter and setup the solver
solver.setup(30);

Compute the T-matrix

Now we are ready to compute the T-matrix of the object.

% determine the order required for the T-matrix
nmax = suggestedorder(kwave,solver.getRadius());
 
% compute the T-matrix
tmat = ghtmatrix(nmax,kwave,solver,0);

Get ROM expansion of the incident field

We will use an incident plane wave travelling in the direction (0,1) ie angle pi/2.

% setup the incident plane wave
inc = plane_wave(pi/2,kwave);
 
% get wavefunction ROM expansion
a = regularwavefunctionexpansion(nmax,0,inc);

Get ROM expansion of the scattered field

The scattered field is obtained from the incident field by matrix multiplication with the T-matrix.

% get wavefunction ROM expansion of the scattered field
b = tmat * a;

Visualise the total field

First we setup a grid on which to plot the total field.

% setup grid for plotting
[x,y] = meshgrid(linspace(-4,4,200));
z = x + 1i * y;
 
% get a mask excluding the obstacle for use plotting
mask = abs(z) > solver.getRadius();

Then the scattered field is obtained from the incident field and the scattered field ROM expansion.

% evaluate total field from ROM expansion and incident field
u = b.evaluate(z,mask) + inc.evaluate(z,mask);
 
% plot the total field
surf(x,y,real(u))

Finally we set the view etc.

% set the view to overhead
view([0 90]);
 
% a few other view options
shading interp
axis equal

The result looks like this: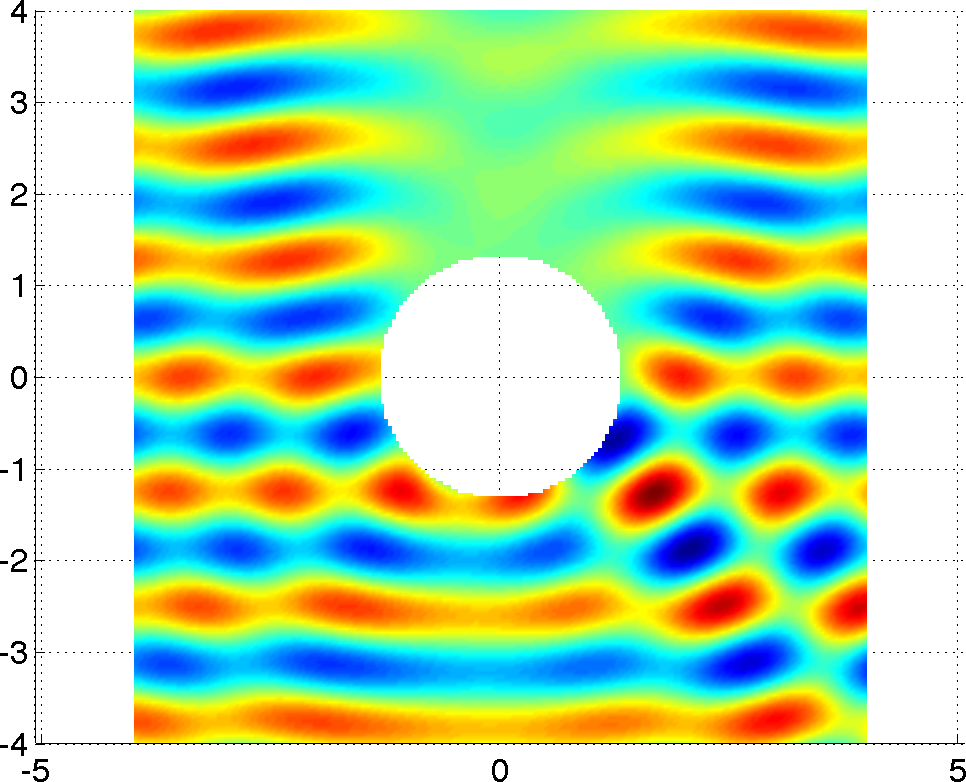

Full code

You can paste the full code into your Matlab command window.

% anonymous functions for radius and its 1st and 2nd derivatives
r = @(t) 1 + 0.3 * cos(3*t);
dr = @(t) -0.9*sin(3*t);
ddr = @(t) -2.7*cos(3*t);
 
% create obstacle object
p = obstaclePolar(r,dr,ddr);
 
% set the wave number
kwave = 5;
 
% create the Nystrom (sound soft) solver object
solver = solverNystrom(kwave,[],p);
 
% set the Nystrom discretisation parameter and setup the solver
solver.setup(30);
 
% determine the order required for the T-matrix
nmax = suggestedorder(kwave,solver.getRadius());
 
% compute the T-matrix
tmat = ghtmatrix(nmax,kwave,solver,0);
 
% setup the incident plane wave
inc = plane_wave(pi/2,kwave);
 
% get wavefunction ROM expansion
a = regularwavefunctionexpansion(nmax,0,inc);
 
% get wavefunction ROM expansion of the scattered field
b = tmat * a;
 
% setup grid for plotting
[x,y] = meshgrid(linspace(-4,4,200));
z = x + 1i * y;
 
% get a mask excluding the obstacle for use plotting
mask = abs(z) > solver.getRadius();
 
% evaluate total field from ROM expansion and incident field
u = b.evaluate(z,mask) + inc.evaluate(z,mask);
 
% plot the total field
surf(x,y,real(u))
 
% set the view to overhead
view([0 90]);
 
% a few other view options
shading interp
axis equal