Up to Scientific notation
As we saw in the earlier examples involving the value of some gold, the number of significant figures in a measurement has an effect on the value of a calculation.
Let's consider another example.
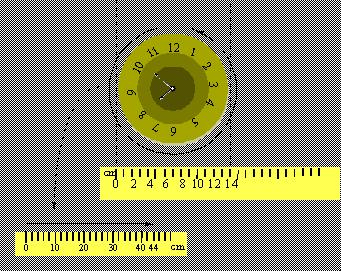
Suppose we measure the diameter of this clock as 14 cm.
Further, we measure the circumference of the clock as 44 cm.
Now we want to find an approximation to the number pi, which is defined as the ratio between the circumference and the diameter of any circle. Reaching for our trusty calculator, we punch in 44 divided by 14.
The calculator spits out the "answer": 3.1428571
Should we trust this answer?
If you have been following the examples up to date, you should suspect that the calculator's answer is a little bit too accurate for the data we supplied. Since we only made the measurements to 2 significant figures, we should only expect the answer to be accurate to same number of figures.
In other words,
On to another example.
Table of Contents